1 = .999…
Q. How many mathematicians does it take to screw in a light bulb?
A. .999…
One of my hobbies is Number Theory. I have a bunch of DVD courses on the topic as well as quite a few books. Consequently, I have always had a secret ambition to write an entire essay consisting of nothing but equations. Mathematics can be so much more beautiful and concise than the words we all struggle to string together. As the language of nature, mathematics has an elegance that far surpasses anything I can try to tap out on my keyboard. So, what do you say; let’s find out if 1 does indeed = .999…
You know what “.999…” means, right? It is a repeating decimal, that means that the 9s just keep going and going; they never, ever stop. So what am I talking about when I say that 1 = .999…? Well, why don’t we take a look at some simple math? I can easily prove to you that 1 and .999…are the same number.
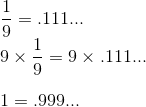
Could the math be any simpler? Interesting, isn’t it? Take a look at this:
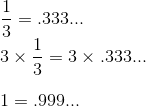
So, are you becoming a believer? The thing about mathematical proofs is that they do as advertised, they prove things. Finally, this proof also gets us there but in a slightly different way.
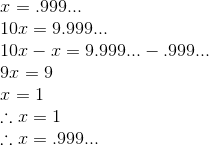
Phil, from Phil’s Slight Oversight fame, read this when he was a college student. He brought it to one of his professors to see if I was doing some sort of magician’s trick just to fool him. His professor told Phil that it is true, 1 does, in fact, equal .999… Phil then asked him if that is so, can he write .999… instead of 1 on a test when it comes up? “Of course,” he replied, “but I wouldn’t do it in any class other than this one.”
Years ago, a high school student named Tayler also read this. She brought it to the attention of her high school math teacher, who immediately told her that I didn’t know what I was talking about. She told Tayler that the idea was nonsense after she spent a few minutes consulting her calculator. Such is life in Iroquois County.
This short post is a prelude to a longer one that is coming next. I will be building on these same principles to reach a bizarre conclusion to a simple math problem about counting. If you are unsettled by this post, I recommend a Google search. What I have done here is just a sample; .999… has its own Wiki page, visit it, and you will find lots of different and varied proofs.
