1:59:40.2
You’ve got to be kidding me. How does a human being run that fast for that long? That’s not possible, is it?
Buford Lister (personal communication)
Years ago, one of my brothers, J, was coaching a high school tennis team. They weren’t necessarily perennial contenders for the league championship. It wasn’t the coach’s fault; this area is not a hotbed of athletic talent. If you could get enough players to come out for the team that was considered a victory. The high school banquet was coming up, and J told me that he didn’t know what to say during his speech. The team only won 2 matches, an improvement from only a single victory the year before. I told him to tell the parents that the varsity doubled its win total, and if that trend continues, they will be undefeated state champions in 25 years. Of course, I was assuming that the win totals would go up arithmetically, not exponentially.
He told the joke, got a big laugh, and then everyone went about their business. I was reminded of that story when I heard what Eliud Kipchoge of Kenya did. He ran an unprecedentedly fast time in a marathon, specific circumstances aside. That speedy performance got me thinking about records, whether they be the win-loss of high school tennis teams or the time it takes to run a certain distance.
So, what exactly did I mean by wins going up arithmetically or exponentially? Take a look at the following figures consisting of a scatterplot with an added trendline. If these fabricated win totals are arithmetic in nature, then the team can count on one additional win per year. On the other hand, if we consider exponential growth, that elusive state championship will come a lot sooner. Such is the power of an exponent as opposed to a plus sign.
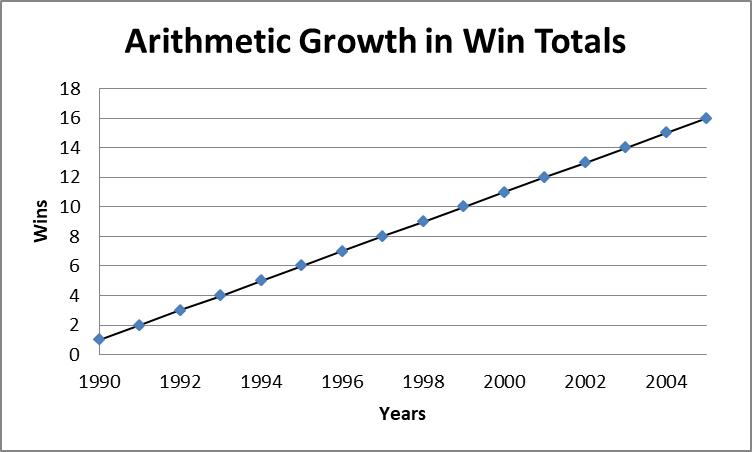
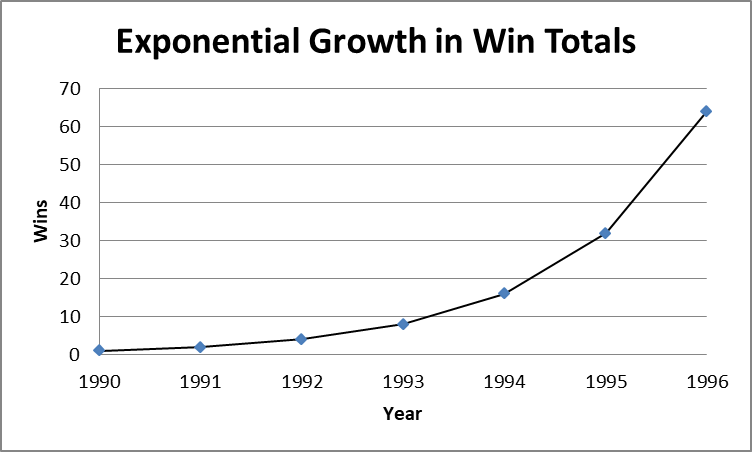
Let’s say he started coaching in 1990 and won one match; the exponential growth curve illustrates that by 1995, the team will win 32. An arithmetic progression would give a paltry total of 6 wins in that same time frame.
Now that we have the introductory stuff behind us, we can get to Kipchoge’s fantastic feat (which, by the way, he accomplished with his feet). A sub-2-hour marathon? Unbelievable. I am truly astonished. I have run 6 of them, and I can’t imagine a person keeping up that kind of pace for 26.2 miles. Exactly how fast was he running? He averaged 4:34 per mile for the entire race. Yes, you read that correctly.
This essay isn’t about Kipchoge; his time speaks for itself. I am not sure I have much expert analysis to offer other than “Wow, that is a fast time.” This post is a mathematical one about linear regression and the slippery nature of extrapolation. No worries, the math is simple even though the ideas are big.
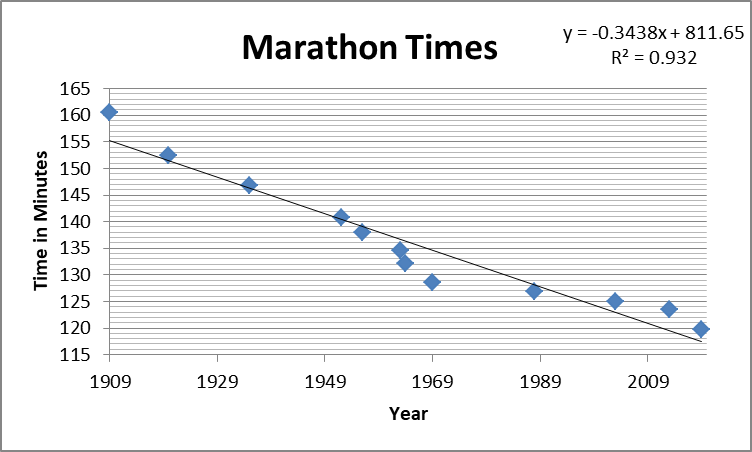
The following figure illustrates the best times in the world for the marathon from 1909 to 2019. Notice how well the data points cluster around the trendline. In this instance, the trendline (the line of best fit) is also known as the regression line.
I dug into the record for the marathon, both official and unofficial. For various reasons, Kipchoge’s time will not be recognized as a world record. That doesn’t mean he was riding a motorized scooter, he did run the distance and finished at the stated time. His time won’t be considered because he had pacers surrounding him, support cars, and a laser projection on the road ahead of him to show his pace. This wasn’t staged as a footrace against other humans, he was only racing the clock. For me, that does not diminish the accomplishment at all, no matter the circumstances, he ran a marathon in under 2 hours.
The scatterplot is set up to show the correlation between the passage of years with the lowering of marathon times. The relationship is strong; see the R2 value in the upper right of the figure? That means that over 93% of the variability found in the marathon times can be explained simply by the march of time. As the years go by, the times go down at a predictable rate; that is what the model is telling us.
You will also notice an equation in the corner of the figure. If we plug in some numbers, we can make some predictions. The equation gives a time of 2:28:07.2 for 1930, the actual record time then was 2:30:57.6. Really close. The model provides a time of 2:21:14.4 for 1950 versus the real record time of 2:20:42.2. As mathematical models go, this one is good; the R2 value of 0.932 is about as decent as it gets when using real-world data.
Now we get to the curious part, we have created a reliable mathematical model of the progression of record marathon times. You know what we need to do, right? We need to extrapolate out into the future to see what times we can expect the best runners in the world to be posting. A few quick calculations give us a fantastic time of 1:29:12 in 2100 and an even more ridiculous time of 55:17.4 in 2200. I don’t think so.
Our model does not consider the physical limits of bone and tendons, the ability of a human to metabolize oxygen, or anything else of that nature. Even though the model is sound, it can’t be used to predict what is going to happen far down the road.
Linear regression, as a mathematical tool, is indispensable to modern statistics. I have done thousands of regressions, and I am always learning something interesting when I enter some data and click that particular button. The trick is to know when the model is telling us something useful and to have the training to realize when there are gaps in our assumptions. There is a reason scientists spend so much time in school. In graduate school, I was often told that nature is a lot smarter than we are. If we want to extract information, we have to be subtle; the object of our interest is exceptionally obstinate. As a general rule: the more careful you are, the better.
Of course, I have a story about linear regression; I will end this essay with it. The method was discovered by the German mathematician Carl Friedrich Gauss, often referred to as the Prince of Mathematicians. Gauss was one of the greatest thinkers who have ever lived.
My story begins sometime in the late 1700s. Gauss is doing Gauss stuff, hanging out, and being a general genius. He had linear regression all worked out, along with the least-squares method essential to the process. Gauss didn’t think much of his discovery, he viewed the math as trivial. I know what he meant; a long time ago, I took a deep dive into regression in a stats class I was taking. The math is elementary, even though it leads to one of the most potent modern statistical tools we have.
Gauss moved on to the dozens of other great discoveries he is credited with. He was a mathematical machine, a child prodigy who more than lived up to all the expectations. He was so busy publishing important work in other areas that he never bothered to let the world know about his discovery of linear regression. We all know what happened, right?
In 1805, along came Adrien-Marie Legendre, a top French mathematician. He got Gauss’ attention when he published a paper called “New Methods for Determination of the Orbits of Comets.” You guessed it; in that paper, he outlined the least-squares method of linear regression. It was on. In science or mathematics, there are few things juicier than a full-on priority dispute.
Gauss wasn’t too impressed with Legendre, he wasn’t going to let the Frenchman have any credit for an idea that Gauss claimed he had years ago. Gauss published a paper in 1809 on the topic of planetary orbits; it included a mention of Legendre’s work, it also has a passage about how late Legendre was to the party. Gauss claimed he had been using the method for over 15 years.
Priority disputes like this one are sprinkled throughout the history of science and mathematics. The most famous probably being the discovery of calculus. Isaac Newton and Gottfried Wilhelm Leibniz, along with their supporters, had a significant tussle over that issue. The fact that such a dispute is taking place is an indication that the idea is important. No one bothers to fight over the uninspired stuff. Linear regression, even though based on simple math, is inspired. I have often wondered why Gauss didn’t immediately see this.
So, what did Gauss do? Did he ultimately give Legendre credit? Not even a little. Gauss was not willing to bend, he refused Legendre even the slightest accommodation. It might surprise you to learn that most historians side with Gauss on this issue. His notebooks show that he had discovered this idea long before Legendre. Curious, isn’t it? Almost always, the person who publishes first gets all the fame and glory. Today, Gauss receives the bulk of the credit for the discovery; if you look hard, you can find Legendre’s name in the footnotes.
I was introduced to linear regression later in life, I came across it in a Ph.D. level statistics course. Today, I hear of elementary school kids who are getting exposed to this technique. They can undoubtedly understand the math, it is that simple. Also, computers can do all the grunt work now. I just hope their teachers are up to the task. I don’t want to see a blue ribbon given to the kid who’s science fair project claims that in 2057, we can expect someone to average a 4-minute mile for the marathon.
