Subtle is as Subtle does, the Strange but True Story of 13 over 27
I have studied lots of different subjects. The most slippery is easy to identify. It is probability theory. Problems in this branch of statistics trip up experts (and me) all the time. There are lots of stories of famous scholars who have gone down in flames when presented with what seem to be straightforward questions about the probability of this or that. This essay is about one such problem.
Let’s imagine that I met a high school classmate at a reunion. When I saw him, I said, “Hey, I hear you have a son; I saw something about him in the paper.” He replied that he has two children, and the oldest is indeed a boy. Now the simple question is: What is the probability that the other child is also a boy?
Well, what are the possibilities? He could have a boy (B) and a girl (G) or a boy (B) and a boy (B). Therefore the probability that both children are boys is 1/2, which is 50%. Take a look at the following table:
BB
BG
GB
GG
Since we know that the first child is a boy, we can eliminate the GB and GG rows. That leaves only two possibilities, BB and BG.
That little scenario is easy to figure out. Of course, it can’t all be that easy, right? Are you ready? Do you hear The Twilight Zone music in the background? What if the guy had told me that he has two children, but he didn’t tell me whether the boy was the oldest or the youngest? What then are the odds that the other child is a boy?
Author’s Note: There are points in some of my essays where the reader’s head might explode. This is just a “heads up.” The following might be one of them.
Let’s go back to our table.
BB
BG
GB
GG
The only possibility that can be eliminated is GG. Therefore (do you see it?), the probability that both children are boys is one in three, or 33.3%. Very strange. Most everyone’s intuition tells them that the probability should be 1/2, that it is a fifty-fifty proposition. When the question is carefully considered, the correct answer is the counterintuitive one.
Probability is subtle; finding the correct answer always depends on meticulously considering all available information. That said, I almost hate to continue. I hope some young student isn’t reading this and immediately decides not to study statistics. Don’t do that! When you develop some mastery over the material, probability theory goes from the counterintuitive to the sublime. It can teach you a lot about how human brains evolved, it can give deep insight into the nature of the mathematical world that we live in…and it can be a lot of fun.
Author’s Note: I will be posting many more essays on probability. Consider this one a bit of a warm-up. Now that the blood is flowing, things are about to get even stranger. Keep in mind how awful human intuition is when it comes to this branch of statistics, and you will be fine. Remember, it’s not you; almost all of us have terrible mathematical intuition.
Our story continues…
I ran into another guy I went to school with. He was always a bit eccentric, and it appears nothing has changed. I said, “I hear you have two children.” He immediately replied, “Why yes, I do. In fact, one is a boy born on a Tuesday.” With that, he turned and danced across the room and out the door.
You guessed it. Now we need to find the odds that the other child is a boy. How subtle can this problem get? The fact that the boy was born on a Tuesday does change the problem, and it certainly impacts the answer. Think about that for a moment. How can it matter at all on what day the boy was born? Let’s find out…
There are 196 possibilities. We get 49 due to the older or younger siblings being born on any of the 7 ways of the week. If you don’t believe me, create a matrix of days of the week with possible births. Such a table is shown below:
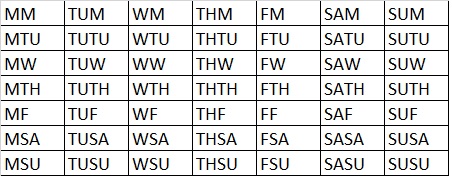
So, if you were to create a matrix with every option, you would end up with:
49BB
49BG
49GB
49GG
Out of the 196 possibilities, we can isolate all of those that have a boy born on a Tuesday. There are 27 cases we can look at that meet this criterion (13 BB, 7 BG, and 7 GB). The 13 BB scenarios are shown below. Therefore the odds of two boys is 13/27. 13/27? 48.1%? Really? Yes, really. Study the table below and it will become clear. It is important to note the overlap on Tuesday / Tuesday (TUTU); we don’t count it twice, giving us 13 instead of 14.
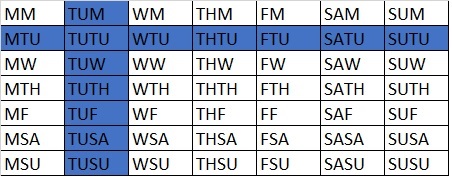
The probability bunny hole is a deep one. The more I study the subject, the more interested I become in the limits of human intuition, especially the mathematical type. It appears we have very little instinct when it comes to numbers, and I don’t think that should surprise anyone. I have a hard time figuring out when insight into subtle probability problems would have been beneficial during our evolutionary history. I don’t see when it ever would have been influential on a genetic level.
Not too bad for an introduction to conditional probability theory. Fairly tame by comparison. Trust me, things are about to get weird. Come along for the ride, it is a bit bumpy (seat belt required), but the destination is worth the trip.