A Little Birthday Math
You say it’s your birthday
It’s my birthday too, yeah
Birthday by The Beatles, written by John Lennon and Paul McCartney
It is about time I drew my attention back to an interesting math problem. This post is about The Birthday Problem, sometimes referred to as The Birthday Paradox. Fair warning, your brain may hurt a little if you go along in this fascinating deep think.
So, the problem is easily stated. If you have a random group of people, what are the odds that two will have the same birthday? Of course, the usual disclaimers apply. The math we will be doing assumes no leap years, no twins (or triplets), and the birth year is ignored. One other implied assumption is that it is equally likely that a person is born on any random day of the year.
What does your intuition tell you? Let’s start here, how large a group would you need for there to be bigger than a 50% chance that any two of them have the same birthday? Most people say that there are 365 days in a year, so the answer must be around 180. You and I both know that answer must be wrong, and it is. As always, there is an inverse relationship between human intuition and probability theory. In this case, a solution of 180 is way off.
The correct answer is 23. Yes, I said 23. Now it is time for a bit of math. I have previously written posts on the “n choose k” method. This tidy formula will tell us how many different combinations of two people we can get from a group of 23. And sure, you can type in “23 choose 2” into Google, and it will give you the answer. Google just told me there are 253 combinations of two that we get from a group of 23. That is a lot more than most people expect.
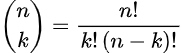
The “n choose k” formula does not help us arrive at the answer of 23; it simply provides a little background for what follows. To answer the question, we will do what mathematicians often do. Instead of calculating the odds that two people have the same birthday, we will do the opposite. It so happens that it is much easier to calculate the odds that the birthdays are different. This is done with the following equation. Once we have that number, we subtract it from 1 to get our answer. After all, the probabilities have to add up to 1, or 100%. For example, if 53% of the people in a group do not have the same birthday, we know that 47% do.
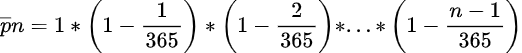
Once the equations are solved, the following chart and graph are easily produced.
People Probability of same birthday
3 0.8%
5 2.7%
10 11.7%
15 25.3%
20 41.1%
21 44.4%
23 50.7%
30 70.6%
40 89.1%
50 97.0%
60 99.4%
You will probably find the results surprising. Once you have a random group of 50 people you can be 97% certain that two of them have the same birthday.
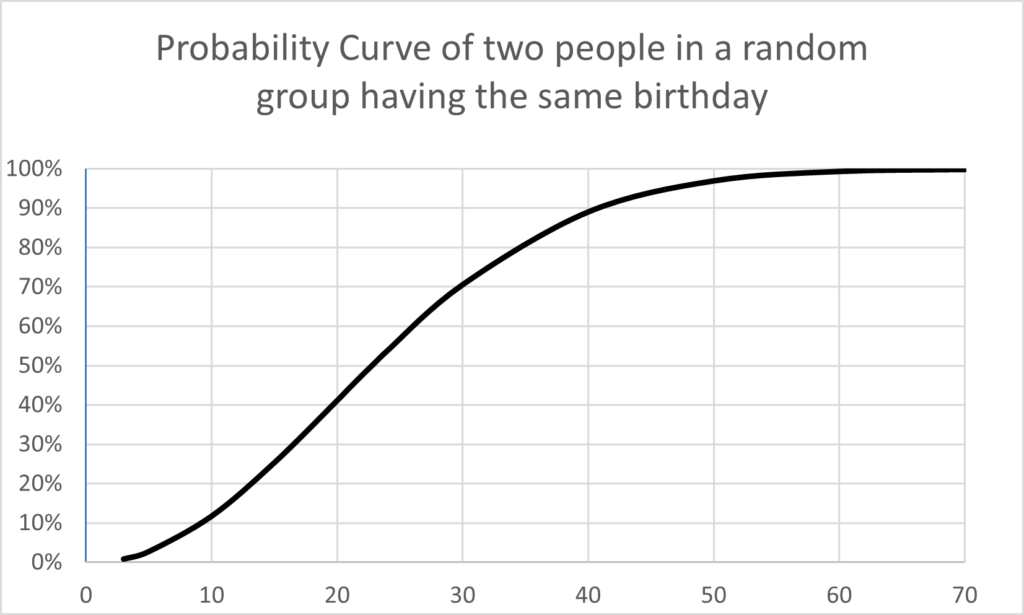
If you study the curve for a few minutes you will see that as you approach 60 people it is virtually certain that two of them will have the same birthday. As is usually the case, our human intuition fails when probability theory is involved. Before doing the math, I wouldn’t have believed this result. It is truly fascinating.
