Phil’s Slight Oversight
Phil was pacing back and forth in his sparse, tiny cell. His mind was racing: man, man, man, man, man…what has happened to me? How did I let it come to this? I don’t belong here, this isn’t right at all.
“Guard, guard! You have to let me out of here. This is a big mistake. I don’t belong here! Do you hear me?”
Jebediah, known to most of the inmates as Big Jeb, approached the cell. He slowly lifted up the index finger of his right hand, pressed it to his lips, and softly said, “shh.”
Phil retreated to his bunk and sat down. He took one of his tennis racquets and slowly pointed it in turn at the pictures meticulously taped on the wall. One photo each for 15 federal indictments. The images were of him and each of his co-conspirators. Shown, of course, in happier times.
So, how does a fine young man like Phil, the stone-cold pride of his hometown, Iroquois City, end up behind bars? My, my, my…what a saga. As with many Shakespearean tales of tragedy, Phil’s story begins long before he was born. This tale of woe starts sometime in 1881 (not really sure of the month) with a man few people have ever heard of, a Harvard trained astronomer and mathematician named Simon Newcomb.
In Newcomb’s day, if anyone needed to know the logarithm of a number, they had to go to a log table book. Thick books composed of nothing but logarithms were commonplace in the days before calculators. I hate to say it, but I can remember consulting them when I was in high school. Anyway, Newcomb noticed that any log table book he looked at had soiled pages at the front while the back pages remained relatively pristine. What this meant is that people were looking up numbers whose first digit was a 1 or a 2 far more than they were searching for numbers that started with an 8 or a 9. Finding this very curious, he wrote up a paper that was instantly (and unceremoniously) ignored by everyone. The astronomer had no idea that about 150 years later, a man named Phil would get arrested because of what Newcomb had discovered all those years ago. I have no further comment; circle of life or some such…at least I guess.
Now we skip ahead to 1938. The plot thickens as a physicist in the employ of General Electric rediscovers what Newcomb noticed all those years ago. Let me be clear about this: What Newcomb discovered is that numbers people were interested in, numbers that came up in their work or studies, started with a 1 or a 2 much more than any of the other numbers. Geez, numbers are numbers, aren’t they? Shouldn’t a number with a leading digit of 1 (e.g., 1,452,325 or 125) appear about 11% of the time when all the possible numbers are considered? I mean, the digits 1 thru 9 should each be represented about 11% of the time, shouldn’t they? That makes nothing other than perfect sense.
Benford, just like Newcomb, was intrigued by those curious soiled pages he found in the various log table books he looked at. Unlike Newcomb, Benford took his discovery much more seriously and analyzed around 20,000 data sets to see if numbers whose leading digit was a 1 occurred naturally more than numbers that started with, say, a 7, an 8, or a 9. Benford studied all kinds of different data sets, any naturally occurring group of numbers he encountered became part of his study. Remember, he was only looking at the leading digits of these numbers. By now, you should be finding this very curious indeed.
Phil wanted to pull his hair out. He kept going over it. Damn, leading digits of numbers…ARE YOU SERIOUS? How was I supposed to think anything different? How was I supposed to know all this? He remembered how he meticulously cooked the books for his investment firm, how he had gone through the spreadsheets very carefully. How could it have never occurred to him that there was a natural pattern that these numbers are supposed to follow? How was it that CurlyMatt or Butera, or anyone who knew what was going on, didn’t know this? Like it is with many people who end up in prison, Phil’s incarceration was simply “one of those things.” In this particular case, though, it was a giant thing, a tragic oversight, a life-changing life lesson.
Phil was escorted into a meeting room, his lead attorney, a tall, lanky man in a bolo tie and a stetson hat, shook his hand and got right to it. “So, Phil, you are not going to like this.”
“C’mon Harky, tell me already. I think I am still paying you by the hour, so get to it.”
“OK, I found this on your bookshelf in the library of your Miami mansion. It was sandwiched in among all the Athena stuff. Remember all those long chapters about the chick some guy met at a rock show? Well, that same guy also wrote this.” Phil took it in his hands and gasped.
“How could I not remember this?”
Harky just shook his head. “Ok, that is all I’ve got. I have to get going. I’ll talk to you soon enough. Just do the best you can, stay safe, and try to remain calm. We are working hard on the appeal.”
Phil shook his head violently. He threw the pages of paper across the room. He yelled so loud that a couple guards rushed to tackle him. After they restrained Phil, this is what one of the guards picked up:
BENFORD’S LAW: A SHORT DISCUSSION
Ryan-Tyler N. Mason
In this brief chapter, I will introduce everyone to a simple yet stunning law of nature. It is called Benford’s Law, and it can be summed up in the following equation: log10 (1 + 1/d). So, what does that mean? Something that I hope all of you find fascinating.
BENFORD’S Law explains a very unusual characteristic found in many, if not most, sets of numbers. The law says that in naturally occurring data sets, e.g., populations of countries, length of rivers, numbers that appear on the first page of any newspaper, numerous untold economic data, etc., the distribution of leading numbers (i.e., the first digit in the number) follows a pattern defined by the equation in the last paragraph. Common sense might suggest to us that the number 1 and the number 9 might show up as leading digits about 11% of the time. Makes perfect sense, right? The following table shows the distribution predicted by Benford’s Law:
1 = 30.1%
2 = 17.6%
3 = 12.5%
4 = 9.7%
5 = 7.9%
6 = 6.7%
7 = 5.8%
8 = 5.1%
9 = 4.6%
Here is the expected distribution of leading digits of numbers in chart form. I include it here so that a sharp distinction can be drawn between natural and unnatural sets, or batches, of numbers.
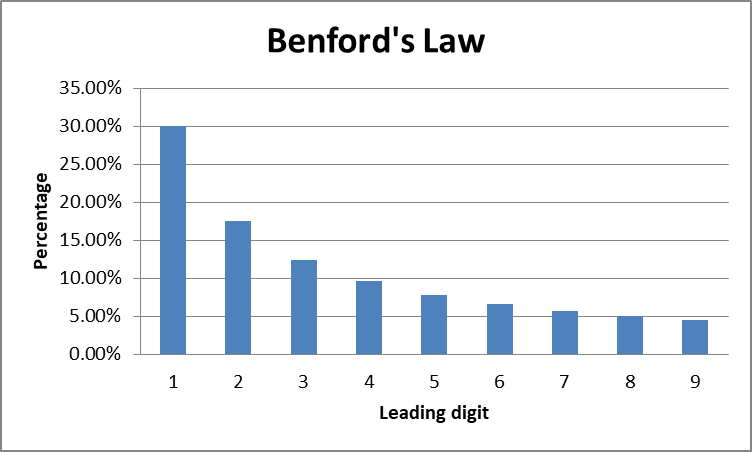
Nature, in fact, does reflect this type of distribution. There are technical reasons why this is true, but I do not want to bog down this discussion with a lot of math. Suffice it to say that Benford’s Law is legitimate and if you really are interested in finding out why further research on this topic can quickly be done on the internet.
Benford’s Law actually has many practical applications. For example, if someone (say a forensic accountant) is hired to go through the financial records of a large company and finds numbers with leading digits that match the distribution found in Figure 1 then no suspicion will be raised. If, on the other hand, a collection looking something like what is displayed in the following bar chart is found, then the CEO and his cronies better find the best criminal defense attorneys money can buy. The type of distribution found here very strongly implies fudged data.
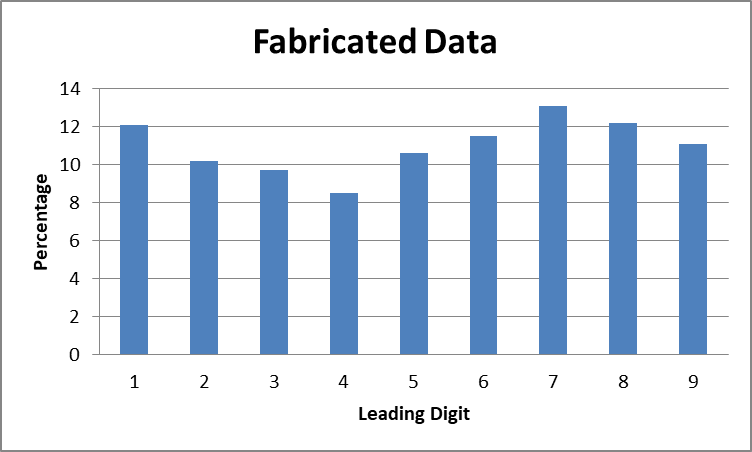
All this information can be obtained just by looking at the first digit of entries in virtually any naturally occurring data set. Isn’t that simply remarkable? Benford’s Law is one of the more curious rules of nature that I have been lucky enough to come across. My only practical recommendation is that if you are going to work in finance or accounting, you need to memorize this law. Phil, I am talking directly to you.
