Negative One Twelfth
There is a perfect epigraph for this essay, but I advise you not to use it. It is too on point. If you think about it, I am sure you can come up with something.
Buford Lister (personal communication)
I have been reminiscing about my time at Harvard University. I admit that for someone who does not like looking back, that is a bit unusual. There is a good reason, though. We will get to that in due time.
As for my experience there, I found that place to be full of the smartest and the hardest working people I have ever known. Nearly all of them had big ideas and the ambition to go along with them. The people I knew cared deeply about making the world a better place. Without question, the time I spent there was the best in my life.
I was “Pahking my cah in Hahvahd Yahd” before the internet took off. The Web was in its infancy; AOL, Prodigy, and CompuServe were all years off. There were only a few sites I could visit with my home built computer (the one with no hard drive and a nine-inch mono screen). There was lots of excitement, though, about how the internet was going to give voice to people who historically did not have one. My colleagues, friends, and associates at Harvard imagined discussions amongst people who would never meet in real life. They envisioned an exchange of ideas that, otherwise, would never have been possible. The hope was that these people from diverse backgrounds would realize they were basically the same, that their similarities outweigh the differences in geography or ideology. There was a kind of magic in the air. There was real hope that democracy would substantially benefit from a thoughtful and nuanced exchange of ideas from people of different backgrounds.
Did you make it through that last paragraph without shaking your head and saying, “Yeah, right!” to yourself? Did you throw up on your shoes? I almost did while writing it because we all know what ended up happening. Nearly every thread I have ever seen on any web page I have ever visited devolved into a racial hate fest within a couple posts. One insult after another hurled by the cowards who hide behind the anonymity that their user names afford them. It really is disappointing; instead of rational and informed discussion, I see lots of intolerance and bullying.
This is the main reason I do not have a social media presence. I have had my fill of hate and, as you know, there is lots and lots of it out there. Trolls, by nature, are always looking to take a negative stance, regardless if they understand the topic or not. I simply do not need it.
So, why THAT introduction? The title (Negative One Twelfth) implies that this might be a math essay, even though I am the first to admit it is curious that the number is spelled out. The other way (- ) seems like it would be cleaner, doesn’t it? Well, this is a math essay. As usual, I am going to bury the lede by taking off on a seemingly irrelevant mathematical tangent.
Let’s start by doing some straightforward calculations and see if we can eventually make our way back to the introduction. Unfortunately (and I do mean UNFORTUNATELY), by the end of this essay, my reasoning will become clear.
We are going to start here: What is: 1-1+1-1+1-1+1…? We will call this SUM1.
[That little string of addition and subtraction has its own particular name. In 1703 Guido Grandi, an Italian scholar, did some interesting work on this problem. As the years went on, other mathematicians started to refer to the problem as Grandi’s Series. Lots of hard and thoughtful work has been done on that simple string of 1s.]
So, do you have an answer? Let’s do what any good, curious mathematician would do; let’s play around with the series and see what we get.
SUM1 = (1-1)+(1-1)+(1-1)+(1-1)… = 0. Fair enough, right?
BUT:
SUM1 = 1+(-1+1)+(-1+1)+(-1+1) … = 1. Now something interesting is happening.
If we solve the series one way, we get 0. If we move our parentheses around, we get 1. So, if you like, we can split the difference:
Angry yet? Probably not, my guess is you are more confused than angry. I can understand why you might not be convinced that SUM1 does equal (it does, perhaps we should look for some better evidence).
Let’s tackle the problem using a different methodology. Consider the following series:
Any guesses where that sequence is going? One way we can solve this problem is by looking at partial sums. We can do that like this:
Do you see what is happening? We are taking the first term, then the sum of the first two terms, then the sum of the first three terms, etc. Our partial solutions are approaching 2, which is the correct answer to the sequence. There is another way (among many) we can solve this problem, and we need to take a look at it.
We can treat the partial sums we just found as a new series, i.e., 1, 1.5, 1.75, 1.875, 1.9375… Now we can take the average of the partial sums in the following way:
We get: 1, 1.25, 1.42, 1.53, 1.61,…
As before, the sequence is moving toward 2. This method, the averaging of the partial solutions, is simply one other way of getting to the correct answer. Got it? Don’t worry if it takes a bit of time to let it sink in. It is a somewhat unusual concept.
Why did I bother bringing this up? Because we can use the same logic to solve SUM1.
SUM1 = 1-1+1-1+1-1+1…
First we get the partial sums: 1, 1-1=0, 1-1+1=1, 1-1+1-1=0, 1-1+1-1+1=1, 1-1+1-1+1=0…
We end up with: 1,0, 1, 0, 1, 0… This does not help much, all we are getting is alternating 1s and 0s. But, as you are about to see, something interesting happens when we average the partial sums. Take a look at this:
Using this method, we find that the sequence is approaching . The further we go out, the closer we will get to
. It has taken a bit of time, but most of you should be convinced that SUM1 =
. If you are still skeptical, I suggest a Google search. The Wiki page on Grandi’s Series is full of useful information.
Here is our next problem, we will now tackle SUM2.
SUM2 = 1-2+3-4+5-6…
This next step is totally legitimate. We are not breaking any mathematical rules. We are simply going to add SUM2 to itself.
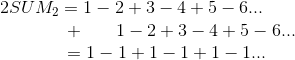
That sequence should be familiar, it is SUM1. Now we can easily solve SUM2.
I am the first to admit that you should be fairly astonished at this point. I know I am.
Now I am going to let you in on a little secret, one that mathematicians and physicists (and me) have known about for a long time. It is a bit of information that makes people very angry. Here we go:
I know, trust me, I know. I came across this little nugget some time ago while taking a course on Number Theory. It didn’t make sense then, and it does not appear to make any sense now, but it is important to note that this result pops up in physics quite a bit. You can find it in String Theory and something called The Casimir Effect (I know a young man who got his Ph.D. in physics from MIT, his dissertation: The Casimir Effect). So yes, if you keep adding numbers forever, you get a negative fraction. Here is the proof:
Easy enough.
Even easier.
So, we now know that 1+2+3+4+5+6+7+8… = Negative One Twelfth. I will admit, the result is slightly counterintuitive. Maybe a little more than “slightly.” Bizarre might be a more appropriate word. I wish everyone reading this the best of luck. It might be helpful to keep in mind that physicists have provided experimental evidence that this solution is correct. Simply astonishing.
I always write these essays intending to use the most straightforward methods possible to introduce the readers to things that I find unusual and fascinating. This Negative One-Twelfth nonsense is undoubtedly a worthy topic. As always, I hope that anyone coming across this essay will become interested enough to do further research. There are lots of blanks to fill in, and a computer search will provide any and all answers you might want. This topic, as you might have guessed, has a fascinating history. Take a look around the internet, you will learn about (among other things) convergent and divergent series, Cesaro Summation, and Abel’s quote that Buford Lister thought was too obvious. If you are genuinely inspired, you will become familiar with the concept of analytic continuation. If you can’t sleep at night because this result hurts your brain, you will be introduced to Leonhard Euler and Bernhard Riemann (true geniuses) and their Zeta Function, a methodology that will also get you to Negative One Twelfth.
I guess it is time to close out this essay. I still owe you an explanation for the introduction. I started the piece the way I did because there are numerous threads out there on this very topic. In general, math and science discussion boards are respectful and informative places where intelligent people discuss the issues of the day. Three Cheers and a Tiger from and for all those Harvard people from so many years ago. Well, you can guess where I am going, right? Discussions concerning this topic get people so riled up that they do little more than fling insults at everyone, including the professors who are trying to explain why Negative One Twelfth is a perfectly respectable (and reasonable) answer to SUM3.
Words such as “stupid” and “moron” are hurled at Ph.D.s by people who have no idea what they are talking about. This is discouraging and totally unacceptable. This problem is elusive; there are instances where Negative One Twelfth is the correct answer, and there might be other instances where it is not appropriate at all. As usual, nature (with all her subtly and nuance) will chime in and let us know when and where to use it.
My final point is that people interested in a problem such as this one are precisely the people who should know better than to head straight to the sewer when they are presented with something they do not understand. Lashing out at people who know more than you about a math or science issue serves no purpose (HACK, HACK, CLIMATE CHANGE, COUGH, COUGH). The internet certainly has given voice to people who otherwise would not be heard, and I am sometimes left wondering just who is benefiting.
