My Favorite President: A Note on The Pythagorean Theorem
Many years ago I had a buddy named Mariah, she was a high school senior working part-time at a restaurant I used to hang out at. One day she approached me to tell me about a paper she needed to write for both her Government and English classes. The topic was a President of the United States, to be assigned at random by the teachers. I immediately said, “Yes!” and started a discussion with anyone who happened by the bar where I was sitting. The question of the day became: Who is your all-time favorite President? The surprising thing is that most everyone had an immediate answer.
As I recall, Mariah was hoping to get assigned George Washington or Theodore Roosevelt, but she ended up with JFK. That turned out OK because I think she learned a few things, and she completed the assignment on time and to the satisfaction of both of her teachers. Sadly, I didn’t get to help her as much as I wanted because she had no internet and I couldn’t get my hands on any drafts. Believe me, I tried, but every time I saw her, she didn’t have her backpack with her, so no draft of her paper was to be found.
So, do you have a favorite President? I sure do, and isn’t it curious that I can write about him within the context of The Pythagorean Theorem. It certainly is mysterious unless you know that one of our former presidents actually came up with a smart and original proof of The Pythagorean Theorem. You had no idea, did you? Trust me, most people don’t.
Before we get to a discussion of James Garfield, I need to take a detour, a pretty big one. I am going to tell you a little about how I write these essays and, in particular, what happened when I started to write this one.
There are many different ways that individual writers approach their craft. I have heard from many sources that Kurt Vonnegut, my favorite novelist, would write three pages of perfect prose in the morning and call it a day. No editing or revision of any kind required. If I tried to do that, I would still be on page one of essay one. I simply could not do it, I am not capable of writing that way.
There is another popular approach to writing called the “scattershot method.” That is exactly how I write. When utilizing the scattershot method, you write whatever comes to mind, you don’t worry at all about grammar, spelling, or punctuation. It is all about ideas and concepts. When I write, I just try to get the thoughts down on paper as quickly as possible. There will be plenty of time to clean things up later, right?
Well, guess what? I have in front of me a sheet of printer paper that contains an outline for this chapter. I got the idea for this essay as I was finishing up one about an interesting algebra problem I stumbled upon. The mechanics of that problem (which will appear in a future post) reminded me of The Pythagorean Theorem. That inspired to write something about the most famous theorem in math, which made me think of the paper Mariah had to write. Get it? It all came together in a flash, so I grabbed a piece of paper and wrote down an outline so that I wouldn’t forget what I wanted to write about. Sigh, much more on that coming up.
Here is a word for word account of what I wrote. I am reading it off the original sheet of paper.
My Favorite President
-Mariah
-Cohen & Newton
-T.R. & Gould
-Garfield & P.T. proof
I include this because I have a huge problem. I understand exactly what everything on there means except for the “Cohen & Newton” segment. Good grief, I know who they are; Cohen is I. Bernard Cohen, the founder of the History of Science department at Harvard University, and Newton is, of course, Issac Newton, arguably the greatest scientist who has or ever will live. The thing is, I have no idea why I wrote their names down. I do not know what I am supposed to say about them, I haven’t a clue as to how either man relates to this essay. I find that a little perplexing.
This is simply more evidence of a disturbing trend, one that I realized a few years ago. One night some time ago, I was reading an article on a topic relating to evolutionary biology. I came across an interesting discussion concerning the biological concept of species. As this was research I was unfamiliar with, I made copious notes in the margin of the paper and went to bed. The next morning I woke up and decided to quiz myself on what I had read the night before. I knew there were three major themes that the author had written about. The big problem is that I could not remember anything about the article. I couldn’t remember who wrote it or what it was about. Yikes, that is not good. I have talked to many other people about this, and they all say that things like that happen to them from time to time, so it is nothing to worry about. I will say this, I don’t find it reassuring that many of my friends might be losing their minds right along with me. Seriously though, I hope they are right, and these gaps in memory are not a big deal. One thing is sure, time, in all its undefeated glory, will eventually chime in with the correct answer.
The fourth line of my infamous sheet of paper reads “T.R. & Gould.” I know exactly what that means, and I can tell you a little bit about that now. That line is about President Theodore Roosevelt and Stephen Jay Gould, the greatest science essayist who has ever lived. Chapter 14 in Gould’s “Bully for Brontosaurus: Reflections in Natural History” is entitled “Red Wings in the Sunset.” It is a neat little essay about Roosevelt’s accomplishments, not as a politician, but as a scientist. Bet you didn’t know that Roosevelt published an important scientific article, did you? Well, he most certainly did.
After he left office, Roosevelt wrote a paper on coloration in birds and mammals. It was published in the Bulletin of the American Museum of Natural History in 1911. The technical details of the article are not important, the point here is that Roosevelt was, at heart, a scientist – ever curious about the world and all its inhabitants. Can you imagine? A former president sat down and wrote over 100 pages about how and why certain animals are colored the way they are. Such a thing could have easily gotten Roosevelt my vote as my favorite president, but as it stands now, he is a close second. Who knows, he may move up to the top spot one day. I am sure his decedents will be sending me fruit baskets with the intention of influencing me.
Now we can get to my favorite president, James Garfield. Garfield was college-educated, he got his degree in mathematics from Williams College. As you are about to see, he put the degree to good use, and that is what makes him my favorite President.
A few years before he became President Garfield, Congressman Garfield came up with a unique proof of The Pythagorean Theorem. The theorem, the most famous in mathematics, states that for any right triangle, the square of side “a” plus the square of side “b” will equal the square of the hypotenuse, known as side “c.” That special relationship has been known for centuries, but Garfield was inspired to find his own proof for why the relationship holds. He did it in a way no one had ever thought of. He proved that a2 + b2 = c2 by taking an inspired look at the area of a trapezoid.
Here is the trapezoid President Garfield used for his proof. It is broken into three right triangles. I love this proof because it is algebraic, you won’t find any geometry in his argument. That makes for an intelligent, and unusual, little proof.
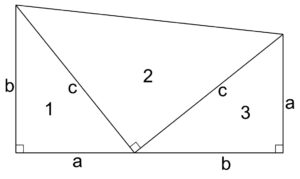
The first thing Garfield did was find the area of the trapezoid. That is easily done in the following way.
Next Garfield, in an ingenious leap, decided to find the areas of the three right triangles. The equations are as follows.
He then took the sum of the areas of the individual triangles as follows.
Since the two areas have to be the same, Garfield simply set the equations equal to each other.
Multiplying each side by 2 gives:
Subtract 2ab from each side:
Simply astonishing. I have to admit that I have a secret ambition (not so secret now) relating to this topic. I want to come up with the worst, most clumsy proof of the theorem that could possibly exist. I want it to be Rube Goldberg-esque, the foulest string of mathematics imaginable, yet I want the proof to be correct. This is the only reasonable hope I have as it appears all the good ones are taken. There are hundreds of beautiful and thoughtful proofs that can easily be found online. President Garfield certainly did his part in that regard. I very much admire his simple, elegant proof.
